Creation Corner
Energy of month redux
In the days since CNAV published an article on the change of the length of the month, something interesting happened. Walt Brown, originator of the Hydroplate Theory, realized he’d overlooked something. This often happens when one proposes a unifying theory to explain all the changes in our world, and the solar system, from one event. Especially an event as violent as the Global Flood.
Brown first wondered whether the moon had lost a fraction of its energy. Then he realized the moon need not have lost any energy at all. The month shortened in line with the decline of the mass of the earth. And that decline explains all the objects in the far reaches of our solar system.
How the month and the earth’s mass relate
Recall the expression for the energy of the moon’s orbit:
where M and m are the masses of the earth and the moon, G is Sir Isaac Newton’s gravitational constant, and a is the semimajor axis (the longest radius) of the orbit of the moon.
The month, or the period of the moon, relates to the semimajor axis thus:
So that:
![a = \sqrt[3]{\dfrac{GMP^2}{4\pi^2}}](https://s0.wp.com/latex.php?latex=a+%3D+%5Csqrt%5B3%5D%7B%5Cdfrac%7BGMP%5E2%7D%7B4%5Cpi%5E2%7D%7D&bg=ffffff&fg=000&s=0&c=20201002)
So:
![E = - m \sqrt[3]{\dfrac{(\pi G)^2}{2}} \left ( \sqrt[3]{M/P} \right )^2](https://s0.wp.com/latex.php?latex=E+%3D+-+m+%5Csqrt%5B3%5D%7B%5Cdfrac%7B%28%5Cpi+G%29%5E2%7D%7B2%7D%7D+%5Cleft+%28+%5Csqrt%5B3%5D%7BM%2FP%7D+%5Cright+%29%5E2&bg=ffffff&fg=000&s=0&c=20201002)
and thus:
Loss of energy includes gain of heat
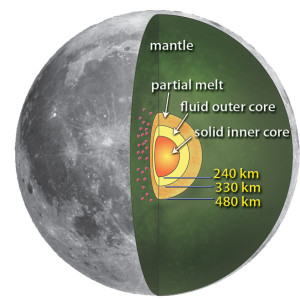
Cutaway of the moon showing the solid-fluid core, partial melt, and mantle, inferred from seismic data from Apollo 14, 15, 16, and 17. Diagram courtesy Renee Weber/NASA
In response to the last article, a regular commenter objected strongly to the notion that the moon lost 0.046 percent of its orbital energy. That would amount to about nine septillion joules. Impacts robbing the moon of that much energy might be only 50 percent efficient. So they would release at least nine septillion more joules, as heat. That could melt the moon, if not smash it to bits.
In fact, many meteoroids, large and small, bombarded the moon after the Flood. Most of these made the craters that all astronomers know. A few much larger ones made lava flow, to form the Great Basaltic Seas of the moon (Oceanus Procellarum and Maria Imbrium, Frigoris, Tranquillitatis, and Crisium on the near or “facing” side, Mare Humboltianum on the eastern edge, and Mare Moscoviense on the far side) and various “bays” of basalt. Obviously that bombardment did release heat, and a lot of it. In fact, the moon has solid and fluid cores, same as earth. But the modern observer has no reason to suppose all or even most of these rocks fell on one side (except for the impactors that formed the maria and sinuses).
How sensitive is the month?
So, as Brown notes today, we have no reason to suppose the orbital energy of the moon changed at all. Therefore the ratio of the mass of the earth to the synodic month (new moon to new moon) did not change during the Flood. So:
To express the pre-Flood month in pre-Flood days, one must convert by a factor of 360/365.256, the ratio of sidereal years in contemporary days before and after the Flood. So:
Substituting 1.03 for the mass ratio and 29.531 (modern) days for the modern synodic month gives an answer of 30 (ancient) days for the pre-Flood month. That’s actually precise to only two significant digits, because we do not (yet) know the mass ratio any more precisely than three significant digits.
Where did all that mass go?
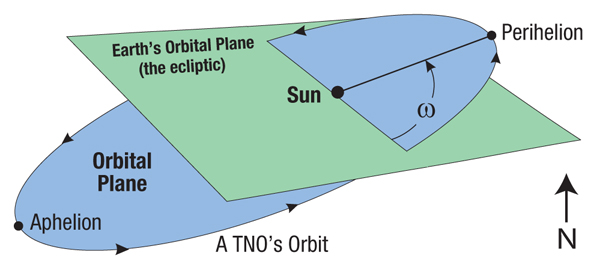
Orbital elements of a satellite of the sun, like a TNO. Note the argument ω of perihelion, the largest bone of contention about the origins of TNOs. Courtesy of Walter T. Brown
The two to four percent of mass the earth lost, is the mass of the Trans-Neptunian Objects. How do we know that? Because in a key orbital element, the argument of perihelion, those objects are strikingly similar. (The argument of periapsis, abbreviated ω, is the arc an orbiting body passes through, after crossing a reference plane, to pass nearest the primary. “Periapsis” becomes “perihelion” when the primary is the sun.)
Megan E. Schwamb noted, in March of this year, that the twelve most distant TNOs all had the same argument of perihelion.
Any formation mechanism proposed for the origin of Sedna and 2012 VP113 [and the other ten most distant TNOs] will need to explain this orbital structure.
Dr. Robert B. Brown is a professor of astronautics at the United States Air Force Academy. (And, incidentally, one of Walter Brown’s sons.) He checked the orbital elements of all 1,346 TNOs. Their arguments of perihelion cluster near either 0° or 180°. The significance of that distribution, per the Chi-Square test, is 99.99 percent. Therefore, some large body, in or near the ecliptic plane, gave all those bodies their greatest push. (The ecliptic is the earth’s orbit around the sun. The plane of this orbit is the most common reference plane in the solar system.)
Which body was it? Not Neptune. Neptune would have been nowhere near most of these bodies in the last 22,000 years, if one assumed an old solar system. And this event must have happened recently. Otherwise all the TNO arguments of perihelion would have spread themselves out evenly. Which would, of course, be the null hypothesis, or what you would expect.
Only one other body remotely qualifies: the earth itself.
Total mass of the TNOs: from two to four percent of the earth’s mass, depending on whom you ask and how they count those objects.
This solves the riddle of how long the month was before the Global Flood, in relation to how long the month, and the day, are today.
Related:
- Energy to change a month
- Energy to change a calendar
- Calendar: from 360 to 365
- Trans-Neptunian objects: from earth?
Terry A. Hurlbut has been a student of politics, philosophy, and science for more than 35 years. He is a graduate of Yale College and has served as a physician-level laboratory administrator in a 250-bed community hospital. He also is a serious student of the Bible, is conversant in its two primary original languages, and has followed the creation-science movement closely since 1993.
-
Clergy4 days agoFaith alone will save the country
-
Civilization2 days agoElon Musk, Big Game RINO Hunter
-
Civilization5 days agoDr. Jay Bhattacharya Will Rebuild Trust in Public Health
-
Civilization5 days agoFreewheeling Transparency: Trump Holds First Post-Election News Conference
-
Civilization3 days agoLegacy media don’t get it
-
Constitution18 hours agoBiden as Feeble Joe – now they tell us
-
Executive2 days agoWaste of the Day: Mismanagement Plagues $50 Billion Opioid Settlement
-
Civilization2 days agoA Sometimes-Squabbling Conservative Constellation Gathers at Charlie Kirk Invitation
Interesting, wish I had the education and math to properly evaluate this.
Jim Levandowski liked this on Facebook.
[…] Energy of month redux […]
C’mon, fellas, you’re giving me whiplash here. First it was 7 giant impacts that slowed the Moon down and turned one face toward Earth, then it was interaction with the Flood debris ‘in orbit roughly parallel to Earth’, and now it’s changed again. Dr. Brown’s previous arguments about this seem to have been removed from his Creationscience.com website, in favor of a constant orbital energy argument. It makes it difficult to clearly rebut claims that have been scrubbed from the record. That’s nice, I guess, since it reflects the fact that you or he realized that the previous model was fictitious. Fortunately, you have preserved some of them here for all to see. It’s annoying, however, in that the target claim seems to be constantly in motion, and surprising given that this stuff had previously been on his website for years, apparently unquestioned.
Still, I’m afraid that this new spin on things doesn’t work either. Dr. Brown wishes to hold the total energy of the Moon’s orbit constant both before and after a claimed Flood that drops the Earth’s mass by ~4% (exact value subject to frequent revision). Before the Flood, with a more massive planet Earth, and with the same lunar orbital energy as today, Dr Brown claims that the Moon’s orbit would have been larger and slower, giving a 30 day synodic month at a time when the days were slightly longer than they are now. Let’s let that sink in for a moment – a heavier Earth, pulling harder on the Moon, purportedly leads to the Moon orbiting slower and farther away than today. Thought experiment time: a tetherball is swinging around a post at a given rate, connected to the post by a strong spring such that the tension in the spring keeps the ball moving in a circle around the pole. The spring is instantly or gradually weakened such that it no longer pulls as hard on the ball for the same amount of stretch. Dr. Brown’s model of the world would suggest that the weaker spring pulls the ball in closer to the pole and causes the ball to rotate more quickly. Does that make sense?
The answer is no, because the energy of the Moon’s orbit before and after the loss of mass from the Earth would not in reality be identical. The total energy of the orbit at any given moment is the combination of two factors: the kinetic energy of the Moon (1/2 mv^2) and the gravitational potential energy of the Moon (-GMm/R). For a circular orbit, the v^2 in the kinetic energy term can be replaced by GM/R, such that the sum of the two terms is [1/2(GMm/R) + -GMm/R], or -GMm/2R as has been mentioned in previous posts. By the way, while I appreciate that the difference between the synodic month and sidereal month happens to be small for the Moon today, the calculations for orbital velocity and energy should really be done with the sidereal values.
What happens to those two terms in the energy equation when mass is suddenly removed from the primary? Well, the gravitational potential energy -GMm/R instantly becomes less negative, because M has suddenly decreased. The kinetic energy of the Moon, 1/2mv^2, is initially unaffected. As a result, the _total_ energy of the new orbit is now _less negative_ than that of the old orbit, because of the smaller -GMm/R term. The Moon’s velocity is now too fast for its old circular orbit. The radial acceleration of the Moon due to Earth’s lesser gravity is now lower than that required to keep the Moon traveling at that velocity in that orbit, so the Moon climbs and slows, losing some kinetic energy in exchange for gravitational potential energy. It is now in a new elliptical orbit that is larger and slower than the old circular one. I went over this in a post a few weeks back. You can’t claim that the energy of the first and second orbits are the same, because the masses of the bodies involved has changed, thus the gravitational potential energy term has changed. It would be like putting a rocket on a satellite, accelerating it, and then claiming that the total energy of the orbit should be the same afterwards. It won’t be; in that case the 1/2mv^2 term has changed, and it’s in _a different orbit_ with _different total energy_.
Let’s take Dr. Brown’s equation of Mbf/Maf = Pbf/Paf at face value. It suggests that for a given Mbf and Pbf, as Maf falls, Paf must also fall. Does it seem physically realistic to say that if 90% of the Earth’s mass vanished, that the Moon would orbit the the remaining 10% with a period 90% shorter as well? Ignoring Roche limits and the like, that the Moon would whip around in a smaller orbit every 3 days? Or if the Earth dwindled to nothing, the Moon’s orbital period would shrink to zero as well?
Of course it wouldn’t, because the equation is false because the orbital energy is not the same before and after the proposed mass loss. In reality, there comes a point where the loss of mass from Earth would make the gravitational potential energy term, -GMm/R, so small that it would equal the kinetic energy term, 1/2(mv^2). At that point, the total energy of the orbit would be zero and the Moon would no longer be gravitationally bound to Earth at all. Its orbit would go from elliptical to parabolic. If yet more mass was lost from Earth, the orbital energy would become positive, and the Moon would leave on a hyperbolic trajectory. If the Earth vanished altogether, the Moon would leave on a straight-line trajectory at a constant velocity. Dr. Brown’s equation claims that the Moon would zip around the non-existent Earth with a period of zero. Wrong.
So: the constant orbital energy bit is unphysical and leads to nonsensical conclusions. If mass is lost from the primary, what actually happens to the orbiting body? It moves out to a larger orbit with a greater period. But you don’t have to take my word for it; you can Google the effect that stellar mass loss has on planetary orbits. Spoiler: as the star loses mass through solar winds, the planets move out to larger orbits. Larger orbits mean longer periods. So today’s synodic period of 29.5ish days would be longer than the pre-Flood period. I guess you’ll have to figure out how to slow the Moon down again after all.
Mopping up some other points:
“Impacts robbing the moon of that much energy might be only 50 percent efficient.” 50% efficiency with inelastic collisions only applies if the two bodies are of equal mass; otherwise the efficiency is much, much worse. For impactors that are 10% as massive as the Moon, the inefficiency is 90%. The bombardment that struck the Moon did release a lot of heat, yes. But over a looong period of time, mostly a looong time ago. It is not possible that the Moon was slowed down by such inefficient bombardment taking place over a few years ~5000 years ago, or it would still be glowing if not coalescing from a ring of vapor and debris. Although now that you have abandoned the impact-slowing theory, perhaps the impacts were merely cosmetic and the efficiency doesn’t matter. Still, the amount of cratering seen on the Moon could not realistically have taken place over a few years within the last 5000 years, or the surface would still be cooling.
“Only one other body remotely qualifies: the earth itself.”
Another claim resting entirely on authority. How does material launched from Earth achieve trans-Neptune orbits? Even if the material was launched from Earth with sufficient velocity to leave the inner solar system, what altered the orbits out beyond Neptune such that it doesn’t return again? Where’s the math?
To clarify the bit about the satellite with a rocket: we are familiar with the concept of changing the total orbital energy of a satellite by altering the kinetic energy term of the equation through the use of rockets or aerobraking or solar sails or suchlike. But changing the total orbital energy by altering the gravitational potential energy term works in the same way. It’s just that we have no day-to-day commonsense experience with altering the mass of the Earth to boost satellites into higher orbits, so we forget about that part of the equation. We could also alter the total energy of the orbit by teleporting the satellite to a different altitude; that would also change the potential energy term, but by changing R rather than M. If the USS Enterprise beamed a low-Earth orbit satellite out to the asteroid belt while preserving its kinetic energy relative to Earth, the gravitational potential energy term would become very small (due to large R) and the satellite would no longer be in a bound Earth orbit. Its total energy would go from -GMm/2R (only true for circular orbits) to zero or positive.
The gravitational potential energy term does not represent the amount of energy released by bringing the mass down from infinity (that would be a positive value in a universe where gravity is attractive). Instead, it represents the amount of energy needed to raise the satellite to an infinite distance. That’s why the term is negative; it represents an energy debt that must be paid to boost the satellite higher. If the Earth disappears, the gravitational potential energy term becomes zero. Satellites in bound orbits have negative total orbital energy because it would require the addition of energy to move them farther from the primary (or would require the primary to lose mass, but that typically doesn’t happen).
Dr. Brown could perhaps now claim that he meant that the kinetic energy of the Moon would remain constant, not the total orbital energy. That energy claim would have the virtue of being true, at least, in the first instants after the loss of Earth mass. Impactors striking the Moon from all different directions with a variety of masses and velocities could be expected to have no net impact on the Moon’s total kinetic energy – or at best have so little net effect as to be ignored. But that doesn’t salvage his claim or make his derived equation valid. A Moon with unchanged kinetic energy but smaller negative gravitational potential energy due to loss of Earth mass must travel in a new orbit with a larger semimajor axis and a longer period. That’s the opposite of the effect that Dr. Brown is claiming. The new orbit won’t be circular, and as a result the kinetic energy and gravitational potential energy terms will vary reciprocally over time, but in such a way that the total orbital energy remains constant at its new value.
Shall we take bets as to what approach Dr. Brown will take next? I suspect that the whole section on the 30-day lunar synodic month will disappear with no acknowledgement. Alternatively, Dr. Brown will ‘realize that he overlooked something’ again and will simply remove the erroneous math claims while leaving in the simple assertion that the synodic lunar month changed due to the Flood.
the rapid revisionism of this article really just serves to undermine the theory. Clearly it was not fleshed out or reviewed very thoroughly.
Started with impactors slowing the moon, then the flood orbital detritus, now the moon didn’t actually need any slowing.
A good theory converges on something, gradually adding in lesser and lesser factors, not routinely replacing the most significant one.
The formula Mbf/Maf = Pbf/Paf is clearly improperly derived as reducing the pull between earth and moon would blatently not result in the moon sinking into a closer orbit just as increasing earth’s mass would not push the moon into a higher period orbit.
I appreciate MatthewJ’s posts on these articles as they are very thorough and well written.
The link posted here:
“So, as Brown notes today, we have no reason to suppose the orbital energy of the moon changed at all.”
no longer points to Dr. Brown’s page referring to the pre-Flood lunar month. Could you please update the link?
I will when it becomes permanent. You see, Dr. Brown does read your comments. When you express yourself as a scientist and make a mathematical case, he takes that very seriously.
I appreciate that.
While we’re waiting, perhaps you will be so kind as to answer a few questions directed toward you, Dr. Hurlbut?
When you first posted about the Flood’s effect on the lunar month in July, did you believe that the case had been adequately made to support Dr. Brown’s claims? If so, do you still believe that?
If you no longer believe that the claim is adequately supported, what was it that changed your mind?
I still believe some event, connected with the Flood, caused the change n the lunar month. The only remaining question is one of detail.
“I still believe some event, connected with the Flood, caused the change n the lunar month. The only remaining question is one of detail.”
No, that’s not how science works. You don’t come to a conclusion then twist the evidence to fit; you look at the evidence and see what conclusions it leads to. The evolution of the Earth/Moon system can be explained perfectly well without bringing in supernatural events and bizarre hypotheses.
Do you deny that Darwinians do the very thing you accuse Dr. Brown and me of doing?
The weight of other evidence for the Global Flood, however strenuously you deny that, makes it a whole lot simpler to solve the problem the Hydroplate Theory seems to have for the change of the month than to fall back on conventional wisdom, which simply cannot hold.
“Do you deny that Darwinians do the very thing you accuse Dr. Brown and me of doing?”
Uh yes, absolutely. Darwin himself was a creationist who changed his mind, and developed his theory, BECAUSE OF THE EVIDENCE.
“The weight of other evidence for the Global Flood”
No it isn’t. There are numerous solid disproofs of the global flood, including the fossil record, the complete absence of any traces of such a flood, the survival of numerous “pre-flood” artefacts and the fact that it’s physically impossible.
No. Darwin absndoned God and from then on looked at the evidence the wrong way.
The fossil record cannot disprove the Flood as long as anyone offers a plausible explanation of that record as an effect of the Flood.
Jim Levandowski liked this on Facebook.