Creation Corner
Global flood astronomical date range

Dr. Walt Brown, nearly three months ago, announced an astronomical fix for the Global Flood. When he did that, he provoked the precise sort of debate scientists ought to have. Brown, with his customary boldness, challenged anyone who doubted him: “Check my math!” Dr. Matthew Jachimstahl, a skeptic (both of the Hydroplate Theory and of the Bible), accepted Brown’s challenge. Brown recently released the full results of that challenge.
A range of dates for the Global Flood.
Your correspondent has copies of all the correspondence between Drs. Brown and Jachimstahl. (In fact, that correspondence began early in July, after Dr. Brown revised his results earlier.) The result of that debate does not change Dr. Brown’s value for the most likely date of the Global Flood. But it does change the standard deviation of that value. The new standard deviation is 100 years. Thus the range of most likely dates for the Global Flood are the year 3290 BC, give or take 100 years.
During the Brown-Jachimstahl correspondence, Brown realized that an independence assumption buried in a standard statistical formula he was using didn’t hold for his comet data. Certain numbers were dependent upon each other. Also, the published “orbital periods” (the time it takes a comet to complete one complete orbit) are not true orbital periods. Instead, they are the periods for osculating orbits.
An osculating orbit (literally, “kissing orbit”) is the orbit an object might follow at any time, if all possible perturbing influences on that object were to disappear. No object follows an osculating orbit, least of all a comet. But osculating periods are the easiest to work with. Changes in osculating orbits and their elements reflect the influences other objects have on them.
But “analytical” solutions still exist to answer the question, “How far off might one be in predicting a closest approach to the sun by projecting any comet’s course backward in time?” Brown explains all his methods here.
How to back-calculate the Global Flood
As ever, Dr. Walt Brown’s Hydroplate Theory says all comets, asteroids, and meteoroids formed at the same time. They formed, furthermore, from water, rock and mud that the Global Flood event launched into space. That launch, of course, happened when “the fountains of the great deep broke open” (Genesis 7:11) in a hypersonic water jet.
Brown used two comets, from the 2008 Catalogue of Cometary Orbits, having these features:
- Long orbital periods
- High inclinations to the plane of the ecliptic (the orbit of earth around the sun)
- Actual records of apparitions (“appearances” of the comets) stretching back at least two thousand years.
- Hundreds of available perihelia, either actual or simulated.
| Comet | Earliest known perihelion: | q | i | Earliest known period | N | Expected error, as σ, to predict: | ||
| Recorded | Simulated | Next Period | Launch Date | |||||
| Halley | 239 BC | 1403.80 BC | 0.586 AU | 162.3° | 69.86 years | 27 | 1.56 years | 130 years |
| Swift-Tuttle | 68 BC | 702.30 BC | 0.9595 AU | 113.45° | 129.33 years | 20 | 2.98 years | 159 years |
Here, q is the perihelion distance,.i is the inclination, and N is the number of periods from the earliest recorded or simulated period, back to the eventual launch date. An AU, or “astronomical unit,” is the average distance of earth from the sun.
The simulated perihelia come from detailed studies of Comets Halley and Swift-Tuttle from the team under Dr. Donald Yeomans. He published these findings separately in the Monthly Notices of the Royal Astronomical Society.
These two studies are part of the first of four steps to arrive at the last result. Briefly, they are:
- Calculate the standard deviation for the change-of-period for each comet. This is the “expected error to predict next period” in the table.
- For each year between 4000 and 6000 years before the present day, compute the sum of squares of the differences between the Julian date at the beginning of the year, and the date of the nearest expected perihelion of each comet. The year in which that sum-of-squares is the least, is the year those comets were closest to earth at the same time.
- Try that again, except start back-stepping from a random point in history for each comet, instead of the earliest known or simulated perihelion. Most desktop computers can do this a million times with ease.
- Now calculate the standard deviation of a normal or Gaussian distribution around that date.
Three ways to define the range of dates for the Global Flood
Walt Brown listed three ways to arrive at the breadth of the date range:
The geometric method is the classic one. For any N, the total error works out to:
σ√[N2+(N-1)2+(N-2)2+…+32+22+1]
Or:
σ√[N(N+1)(2N+1)/6]
This formula, for each of the two comets, gives the values in the “Expected error to predict launch date” column. The reciprocal of the square of the combined error is the sum of the reciprocals of the squares of the individual errors. That result is 100 years.
Brown also lists the algebraic and Monte-Carlo methods to find this error. All three methods give the same answer: 100 years.
How remarkable is this date range for the Global Flood?
This graph (from Brown’s Technical Notes) shows how remarkable the middle of the Global Flood date range is. It is a semi-log plot showing the sum-of-squares of the differences in time of the perihelia of the two comets from any given date, as a function of years before present. This plot forms several downward spikes at somewhat regular intervals. But at 3290 BC, the spike extends significantly lower than average.
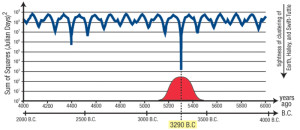 Dr. Jachimstahl raised another issue: why search between 4,000 years and 6,000 years before the present? Why not go as far back as a million years? Might not similar tight convergences happen at regular intervals, perhaps 12,000 years apart?
Dr. Jachimstahl raised another issue: why search between 4,000 years and 6,000 years before the present? Why not go as far back as a million years? Might not similar tight convergences happen at regular intervals, perhaps 12,000 years apart?
But in proposing that, Dr. Jachimstahl ignored a fundamental fact about comets. They die. When a comet no longer displays its plumage on its approach to the sun, or displays so little of it that we on earth cannot see it anymore, we say that comet is dead. The problem: comets that come within one AU or closer to the sun, die after a hundred close passes.
The earliest known period for Comet Halley (see the table) is 69.86 years. Thus if Comet Halley was older than about 7,000 years, it would be dead today. But in its last apparition (1986), it showed its plumage as brightly as it did in 1066, when Londoners stared at it in shock and awe shortly before William the Conqueror really showed them what shock and awe felt like.
So the best place to search for a common launch date of the material that became the comets, must fall within the interval of the longest possible life of the comet with the shorter period. If that comet is “alive” today, then one cannot search back to a time before said comet was “born.”
To do otherwise, one must further assume that the Oort cloud exists, and that Comets Halley and Swift-Tuttle both fell out of it. But the Oort cloud has a deal-killer already: too many comets making their closest approach to the sun at less than 3.0 A.U. Including both Comets Halley and Swift-Tuttle. That holds also for comets having short periods, on the order of those for Halley and Swift-Tuttle. (This table compares the Hydroplate Theory to all other theories of where comets came from, and lists all deal-killers.)
What this means for Bible scholarship
This correspondent calculated twenty-four possible dates for the Global Flood, based on alternative theories for:
- The chronology of the Kings of Israel and Judah following Solomon’s reign,
- The chronology of the Sojourn in Egypt,
- The chronology of the life of Terah, father of Abraham, and
- The use of three different manuscript sources of the ages of the Patriarchs.
Five of the twenty-four dates for the Global Flood fall within the two-hundred-year range 3290 BC ± 100 years.
- All five are consistent with the long chronology of the Sojourn in Egypt.
- Four of the five are consistent with the Septuagint (LXX), and one with the Samaritan Pentateuch (SP), for the ages of the post-Global Flood patriarchs when each sired his next named son.
- Three of the five are consistent with the long chronology for the birth of Abraham.
- Three of the five (though not the same three) are consistent with the Ussher/Lloyd chronology of the Kings of Israel and Judah.
The most remote of these five dates (3343 BC) still falls well within this range, at 3290 BC plus about one-half sigma before then.
[subscribe2]
Terry A. Hurlbut has been a student of politics, philosophy, and science for more than 35 years. He is a graduate of Yale College and has served as a physician-level laboratory administrator in a 250-bed community hospital. He also is a serious student of the Bible, is conversant in its two primary original languages, and has followed the creation-science movement closely since 1993.
-

 Executive4 days ago
Executive4 days agoSecret Service chief gets no solace
-

 Executive3 days ago
Executive3 days agoWaste of the Day: Louisville Taxpayers Pay Nearly $600,000 For Empty Building’s Maintenance, Security
-

 Guest Columns4 days ago
Guest Columns4 days agoFear Itself: Democrats’ Favorite Strategy Caused Their Current Chaos
-

 Executive3 days ago
Executive3 days agoWhere is Joe Biden – or Jill?
-

 Executive1 day ago
Executive1 day agoWaste of the Day: Throwback Thursday: Cities Used Crime Prevention Funds on Soccer Games, Paper Shredding
-

 Executive2 days ago
Executive2 days agoFacile and politically motivated suggestions
-

 Civilization5 days ago
Civilization5 days agoBuild Iron Dome in the United States To Prepare for Israel’s Worst Day
-

 Executive4 days ago
Executive4 days agoThe Emerging GOP Plan To Beat Kamala Harris













Sorry that I missed this when you first posted it. Can you tell me what your evidence is that a comet dies after a hundred close passes to the sun? NASA believes that Halley, for example, has made about 2300 passes and has about 2300 more left to go before it breaks up or vanishes altogether: link to adsabs.harvard.edu..103H
I think NASA is revising some of its criteria to account for Comet Halley’s continued brightness and plumage. This is of a piece with a lot of goalpost-moving that conventional astronomers have made in the last twenty or thirty years.
Well, comet Halley is about 8x8x15 kilometers in size, and on its last few orbits it has lost about 1/1000 of its mass per orbit. Projecting back in time, the percentage of mass loss per orbit would be smaller. So why should we believe that the comet has a lifespan of only 100 orbits? Comet Hale-Bopp is about 60 kilometers in diameter – how much mass would it have to lose each orbit to go extinct in just 100 orbits? Hale-Bopp also lost about 1/1000 of its mass over its last orbit.
So where is the goalpost-moving? Where is the evidence that comets go extinct after ~100 orbits?
A comet wouldn’t have to lose all its mass to die. A comet dies when you can’t see it with the naked eye.
No, it’s not extinct when it’s no longer a naked-eye object, but that’s beside the point. Nor does the comet have to lose all its mass to go extinct, as you said – just enough of its volatiles such that the dust on the surface insulates the remaining ices sufficiently that no major outgassing occurs. I think you’ll find that any reference that points to comets going extinct after ~100 orbits also assumes ~1% mass loss per orbit (the absolute mass loss per orbit falls off over time but the percentage stays about the same). If you can find a reference to comets with 0.1% mass loss/orbit going extinct that quickly, then I will stand corrected.
Anyway – do you think that there will be any more upcoming corrections to the cometary calculations?
When the team of Donald Yeomans, or some other team, back-calculates another comet to well before the Birth of Christ, Dr. Brown and I will look at it again.
Not until then? Even though the formula that he is using to calculate the standard deviation of his derived Flood date is wrong?
I don’t accept the premise.
Well, I don’t accept his premise either, so I guess we agree?
Still, he’s convinced that the closest convergence date lies halfway between the 27th Halley and 20th Swift-Tuttle perihelia, as counted back from their earliest known computer-modeled perihelia. So he should be looking for the standard deviation of the mean of two random variables X and Y (in this case, the dates of the aforementioned 27th Halley and 20th Swift-Tuttle perihelia). X and Y have known standard deviations of their own, which come from that σ√[N(N+1)(2N+1)/6] equation that Dr. Brown has already revised at least once.
Hey, do TEX markups work here? I’ll try: \sigma \sqrt{\frac{(n)(n+1)(2n+1)}{6}} I guess we’ll find out.
The mean of two random variables X and Y is (X+Y)/2, or 0.5X + 0.5Y.
Quick review of the algebra of random variables: the variance of the sum of two random variables X and Y, Var(X+Y), is Var(X) + Var(Y). The variance of a random variable X multiplied by a constant b, Var(bX), is b^2(Var(X)). Finally, the variance of the sum of two random independent variables multiplied by constants, Var(aX + bY), is a^2(Var(X)) + b^2(Var(Y)).
Therefore the formula for the variance of the mean of X and Y in this case is:
Var(0.5X + 0.5Y) = (0.5)^2(130)^2 + (0.5)^2(159)^2
and the standard deviation is the square root of the variance, so
stdev(mean of X and Y) = sqrt[(0.5)^2(130)^2 + (0.5)^2(159)^2]
Not that I agree with his conclusion that the date of closest convergence can be pinned down to the mean of those two perihelia; the real sigma for this problem can’t be calculated this way; the underlying premise is flawed; etc. etc., but at least this version of the equation is internally consistent with Dr. Brown’s Weltanschauung.
Charlotte Laborde liked this on Facebook.
[…] 5300 years? Because the Biblical Flood Event took place that long ago. The orbits of the comets (especially Halley and Swift-Tuttle) tell us […]